Rechenmeister

Zahlen werden in Handschriften des abendländischen Mittelalters bis ins 13. Jahrhundert ausschliesslich in antik-römischen Zahlzeichen geschrieben. Später erhalten diese immer erfolgreichere Konkurrenz von den uns geläufigen arabischen Zahlzeichen indischen Ursprungs. Die Null und das Stellenwertsystem werden durch arabische Rechenlehren im 12. Jahrhundert verbreitet.

Im Rahmen des Unterrichts an kirchlichen Schulen werden bereits früh Rechenkenntnisse in bescheidenem Umfang vermittelt. Das Einmaleins reicht oft nur bis 5x5 und wird durch Aufsagen im Chor gelernt. Für das praktische Rechnen benutzt man römische Zahlzeichen. Die Division und das Bruchrechnen werden mit Hilfe einer Tabelle (Calculus) ausgeführt, der man die Vielfachen ganzer und gebrochener Zahlen entnehmen kann. Vom Ende des 10. Jahrhunderts bis etwa 1250 wird das Rechnen im Klosterbereich meist mit Hilfe des Abakus durchgeführt.
Im Spätmittelalter findet eine grosse Zahl von «Algorismus»-Schriften Verbreitung. Sie lehren die Darstellung natürlicher Zahlen durch die indisch-arabischen Ziffern und das Rechnen mit ihnen in den vier Grundrechenarten, dem Wurzelziehen sowie einfachen arithmetischen und geometrischen Folgen. Rechenmeister verbreiten das neue indisch-arabische Ziffernrechnen in Schulen und Rechenbüchern. In diesen wird noch im 16. Jahrhundert neben dem schriftlichen «Rechnen mit der Feder» das «Rechnen auf Linien» gelehrt.

Aus: Gottfried Keller, Der Grüne Heinrich. Erste Fassung, 1. Buch, 6. Kapitel, Frankfurt a.M. 1978, S. 101f.

«Sie konnte nur gebrochen Gedrucktes lesen, hingegen weder schreiben noch in arabischen Zahlen rechnen, welche letzteren es ihr nie zu kennen gelang; sondern ihre ganze Rechenkunst bestand in einer römischen Eins, einer Fünf, einer Zehn und einer Hundert ...Sie führte kein Buch und besass nichts Geschriebenes, war aber jeden Augenblick im stande, ihren ganzen Verkehr, der sich oft auf mehrere Tausende in lauter kleinen Posten belief, zu übersehen, indem sie mit grosser Schnelligkeit das Tischblatt mittels einer Kreide, deren sie immer einige Endchen in der Tasche führte, mit mächtigen Säulen jener vier Ziffern bedeckte. Hatte sie aus ihrem Gedächtnisse alle Summen solchergestalt aufgesetzt, so erreichte sie ihren Zweck einfach dadurch, dass sie mit dem nassen Finger eine Reihe um die andere ebenso flink wieder auslöschte als sie dieselben aufgesetzt hatte, und dabei zählend die Resultate zur Seite aufzeichnete. So entstanden neue kleinere Zahlengruppen, deren Bedeutung und Benennung Niemand kannte als sie, da es immer nur die gleichen vier nackten Ziffern waren und für Andere aussahen, wie eine altheidnische Zauberschrift.»

Die römischen Zahlzeichen werden während des gesamten Mittelalters im Westen benutzt, um Zahlen darzustellen.
I = eins
V = fünf
X = zehn
L = fünzig
( = einhundert
I) = fünfhundert
(I) = eintausend
Nach der Einführung des Buchdrucks wird das Zeichen «(» zu C, «I)» zu D und «(I)» zu M. C, D und M kaschieren die rekursive, exponentielle Möglichkeit, zehntausend als «((I))», hunderttausend als «(((I)))» usw. darzustellen. Dennoch sind die elementarsten Berechnungen mit römischen Ziffern mühsam.
Beispiel: Multiplikation XXII mal CXXXI. Der eine Faktor wird in seine Bestandteile zerlegt senkrecht angeschrieben:

Die komplizierte Handhabung macht das römische System als Medium für Berechnungen praktisch unbrauchbar. Deswegen werden Rechnungen am Abakus ausgeführt. Allerdings wechseln noch im 15. Jahrhundert in den Handelsbüchern römische und arabische Ziffern ab. Erst der Buchdruck verhilft den indisch-arabischen Ziffern zum Durchbruch. In seinem Roman «Der grüne Heinrich» schildert Gottfried Keller noch im 19. Jahrhundert eine alte Trödlerin, die nur stockend Gedrucktes lesen und weder schreiben noch in arabischen Zahlen rechnen kann. Dennoch kann sie mit einer Kreide auf dem Tisch mit den römischen Zahlzeichen I, V, X und C geschickt rechnen:

Prima per se, secunda decem, [dat] tercia centum,
Quarta dat mille, sed quinta milia decem,
Sexta dat centum, dat septima milia mille,
Centesies nona dat figura milia mille,
Millesies mille milia decima tibi signabit.

Hexameter um 1460 geben den Wert an, den die Ziffern je nach ihrer Stelle besitzen.
Herzog August-Bibliothek, Wolfenbüttel, Cod. Guelf. 1189 Helmst., fol. 189.

Früheste Belege für die Verwendung indisch-arabischer Ziffern im Westen stammen aus dem 10. Jahrhundert. Die weitere Verbreitung beginnt erst mit der Übersetzungstätigkeit aus dem Arabischen im 12. Jahrhundert. Allerdings werden Zahlen in Handschriften bis ins 13. Jahrhundert ausschliesslich in den antik-römischen Zahlzeichen geschrieben. Noch 1299 verbieten die Behörden in Florenz den Kaufleuten die Verwendung der neuen Ziffern in ihren Büchern wegen einfacherer Fälschungsmöglichkeit. Auch auf Münzen finden die indisch-arabischen Ziffern erst spät Eingang.
Verständnisschwierigkeiten bereitet vor allem die Idee des Stellenwertes und die Bedeutung der Null, die einerseits für «nichts» steht, andererseits aber den Wert einer Ziffer verzehnfachen kann. Um das neue Zahlsystem begreiflich zu machen, werden Erläuterungen in Versform ersonnen, die die Ziffernformen erklären oder Namen und Wert der Ziffern veranschaulichen. Schliesslich setzen sich die neuen Zahlen in den Rechenstuben der Kaufleute durch, weil sich indisch-arabische Zahlen besser zum Rechnen und für die Buchführung eignen, was der Abakus nicht leisten kann. Der endgültige Durchbruch gelingt mit der Einführung des Buchdruckes.

Die Schwierigkeit des indisch-arabischen Zahlsystems im Vergleich zum römischen besteht in der besonderen Verwendung der Null. Dieses Zeichen beeinflusst den Wert der Ziffern, kann zum Beispiel eine Zahl verzehnfachen, besitzt aber keinen Eigenwert: Gleichsam ein Metazeichen und doch eine Zahl. (Brian Rotman)
Dies ist für mit dem Abakus rechnende Abakisten eine schwierige Vorstellung. Sie spiegelt sich im Etymologischen: Aus dem arabischen Ausdruck «sifr» für die Null wird im Abendland einerseits «cifra-Chiffre-Ziffer», andererseits «zefirum-zero». Sogar für Teufelswerk wird die eigentümliche Null gehalten. Sinngemäss lautet eine Spottzeile aus dem 16. Jahrhundert: «Wie die Puppe ein Adler sein wollte, der Esel ein Löwe, die Äffin eine Königin – so wollte die Null eine Ziffer sein.»

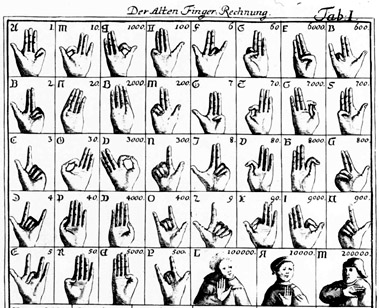
Neben den römischen und indisch-arabischen Ziffern gibt es noch eine andere Art der Darstellung: Die Zahlen 1 bis 10'000 werden durch verschiedene Stellungen und Beugungen der Finger angezeigt, wobei die Einer und Zehner in der linken, die nächsten beiden Stufen in der rechten Hand gebildet werden.
Fingerzahlen sind bereits in der Antike bekannt. Spätere Beschreibungen stammen unter anderem von Beda Venerabilis (674 bis 735). Bei der bis in die Neuzeit gängisten Methode des Rechnens, dem Kopfrechnen, dienen die Fingerzahlen als mnemotechnisches Hilfsmittel zum Festhalten von Teilergebnissen. Auf diese Weise können aber nur einfache Rechenaufgaben gelöst werden. Die Bedeutung der Fingerstellungen ist interkulturell verschieden.

Der Abakus, das Rechenbrett, erleichtert besonders beim Fehlen einer positionellen Zahlenschreibweise das Rechnen. Ein Abakus besteht aus einer Anordnung von Rillen oder Drähten, die eine aufsteigende Serie von Reihen bestimmen, auf denen Zählkugeln oder andere Zeichen plaziert sind. Die Kugeln der untersten Reihe stellen die Einer dar, die nächste Reihe die Zehner usw. Mittelreihen bedeuten eine fünf, fünzig usw. Die Ziffer MMMDCCCLXXXII entspricht folgender Stellung auf dem Abakus:

Im späten Mittelalter ist der Linienabakus sehr beliebt. Davon zeugen unzählige Rechenpfennige (13. bis 18. Jahrhundert), einige Rechenbücher und wenige erhaltene Rechentische. Bis in die Renaissance bleibt das Rechnen auf dem Abakus das gängigste Verfahren, nicht zuletzt weil es auch von Lese- und Schreibunkundigen ausgeführt werden kann.

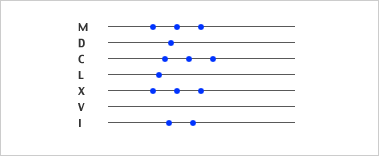
Das Lininenrechnen, eine besondere Form des Abakusrechnens, wird im Mittelalter als einfacher angesehen als das schriftliche Rechnen.
Fünf, sieben oder mehr Linien werden auf eine Unterlage gezeichnet. Auf der ersten Linie, mit einem «x» gekennzeichnet liegen die Einer-Rechensteine, auf der nächsten die Zehner usw. Die Zwischenräume bedeuten fünf Einheiten der unteren Linie: 5 Rechensteine der Einerlinie sind durch 1 Rechenstein im Zwischenraum zwischen Einer- und Zehnerlinie zu ersetzen. Dieses System lässt sich auf weitere Zehnerpotenzen ausdehnen, zum Beispiel 1977:

Will man 73, 65, 103 und 14 addieren, so legt man zunächst die einzelnen Zahlen nebeneinander und fasst dann zusammen:
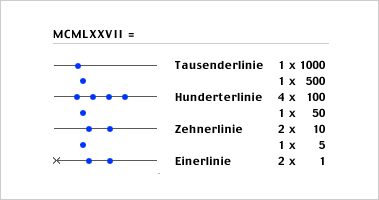
In der Einerlinien befinden sich 3+3+4 Steine, das bedeutet: 10 Steine sind durch 1 Stein auf der Zehnerlinie zu ersetzen.
Auf der Zehnerlinie befinden sich dann 2+2+1 Steine: Das ergibt einen Stein im Zwischenraum zur Hunderterlinie.
Nun liegen 3 Steine in diesem Zwischenraum: 2 davon werden durch einen Stein auf der Hunderterlinie ersetzt und schon kann man das Ergebnis 255 ablesen.